2021. 6. 1. 20:49ㆍAI Paper Review/Deep RL Papers [EN]
<arxiv> https://arxiv.org/pdf/2101.03958.pdf
0. Why Designing Reinforcement Learning Algorithms Are Important?
"Designing new deep reinforcement learning algorithms that can efficiently solve across a wide variety of problems generally requires a tremendous amount of manual effort" -Evolving Reinforcement Learning Algorithms-
1. Designing Reinforcement Learning algorithms
Deep Reinforcement Learning is often used for AutoML such as Neural Optimizer Search, Searching For Activation Functions, Neural Architecture Search. In AutoML, RL often outperforms human-designed algorithms. But designing RL itself is somewhat limited. RL has different design choices compared to supervised learning, such as formulation of reward, policy update rules, exploration, etc.
2. Evolving Reinforcement Learning Algorithms
Evolutionary methods such as Genetic Algorithm(GA) are often used in AutoML, Hyperparameter Optimization including RL. This paper derives reinforcement learning algorithms with the evolutionary methods, especially in task-agnostic value-based RL update rules.
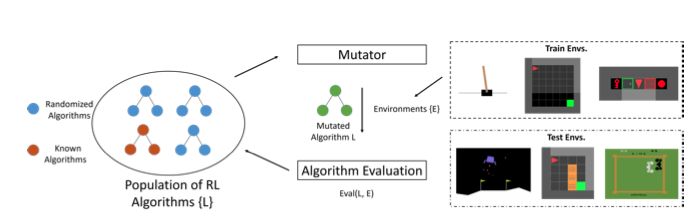
2.1 RL algorithms are derived as mutatable computational graphs.

2.2 Objective of meta-learner
This method tends to find value-based discrete RL algorithms, so it finds the update rule (Loss to minimize) of the q-function which can maximize the return.
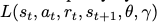
This method is for developing task-agnostic RL algorithms, so we are evaluating the sampled algorithm in a set of environments. To scale the reward, this method normalizes the return via max reward of environment and min reward of environment, which is assumed to be known.

so the full-objective for meta-learner is to learn loss function L which gives maximal normalized average training return over the set of training environments.

3. evaluation & evolution loop
The training loop(the evaluation loop for Loss function) is really typical. we use epsilon-greedy for exploration, update the q-function, store transition.

Before explaining the evolution loop, let's take a look at the nodes. We have three types of nodes.
1. Input nodes
represents inputs to the function, such as discount factor, elements from transition
2. Parameter nodes
are neural network weights, for the approximation for the q-network
3. Operation nodes
are computation nodes, such as basic numerical operations, linear algebra, etc. the inputs and outputs of nodes are typed among (state, action, vector, float, list, probability), this reduces the search space, also allows for this method can be domain-agnostic.
There is a combinatorially large number of graph configurations. plus, the evaluation step is computationaly heavy, takes a long time compared to supervised settings. so, this method applies four methods to reduce time.
- Functional equivalence check via random inputs
- Early hurdles. For example, this method terminates rapidly failing agents.
- Program checks. Basic checks to rule out and skip training invalid programs. For example, the loss function needs to be a scalar value
- Bootstrapping vs From Scratch. given the base algorithm(DQN) convergence can be fast.

4. results
4.1 training has been done on 300 CPUs, 20000 algorithms have been evaluated for roughly 72 hours.
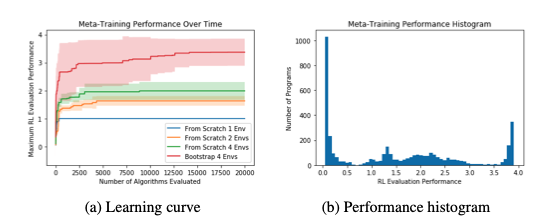
4.2 Learned algorithms
In this paper, a number of training environments over the experiment. for the two-environment training setup(Cartpole and Lunarlander) learns the known TD loss from scratch, which is quite surprising.

while single-environment setup learns variation which does not use the discount. this indicates that the range of difficulty in the training environments is really important
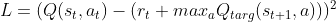
meanwhile, in the bootstrapped version of the experiment, this method found some improvements of the DQN. which is DQNclipped, and DQNReg, which has good generalization performance on the test environments.


Intuition for the resulting algorithms is similar, which regularizes the Q value to be lower. While the overestimation problem is a big issue in DQN, regularizing Q value, which DQNReg and DQNClipped do, can deal with this problem.
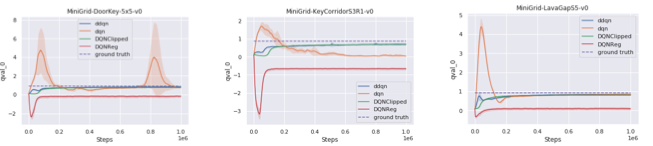
As a result, DQNReg and DQNClipped outperform DQN and DDQN in many environments.

Disclaimer:
This is a short review of the paper. it only shows a few essential equations and plots.
If needed, always read the full paper :)
Materials & Previous Works that you need to understand this post:
0. Reinforcement Learning: An introduction (Richard Sutton)
1. Playing Atari With Deep Reinforcement Learning (Minh et al)
2. Deep Reinforcement Learning with Double Q-Learning (Hasselt et al)
3. AutoML-Zero: Evolving Machine Learning Algorithms From Scratch (Real et al)
4. Neural Architecture Search with Deep Reinforcement Learning (Zoph et al)
'AI Paper Review > Deep RL Papers [EN]' 카테고리의 다른 글
| [3줄 RL] SMiRL: Surprise Minimizing Reinforcement Learning in Unstable Environme (0) | 2021.07.02 |
|---|---|
| WHAT MATTERS FOR ON-POLICY DEEP ACTOR-CRITIC METHODS? A LARGE-SCALE STUDY (0) | 2021.06.16 |
| Decision Transformer: Attention is all RL Need? (0) | 2021.06.12 |
| Munchausen Reinforcement Learning (0) | 2021.05.31 |
| Self-Imitation Advantage Learning (SAIL) (1) | 2021.05.31 |